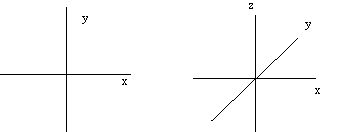
We will need to graphically analyze many of our systems, if only for the purpose of making sure that we understand the problem we are to solve. It is important to carefully define the coordinate system we use, since it will provide the means to consistently measure the quantities we wish to include in our computations. A coordinate system is defined by three things: an origin, the directions of the axes, and a distance scale (which is usually but not always the same for each axis). We typically use the variable "x" to denote a spatial coordinate in a one-dimensional system, the variables "x" and "y" to denote spatial coordinates in a two-dimensional system, and the variables "x", "y" and "z" for the spatial coordinates in a three-dimensional system. These variables coincide with the standard, mutually perpendicular Cartesian axes:
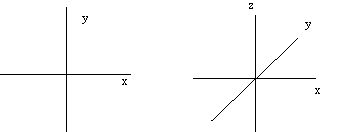
In addition, our coordinate system will always include a time coordinate, typically denoted by the variable "t", whose origin typically is at the beginning of the experiment.
Just as a negative spatial coordinate locates an object on the negative half of its axis, so too negative values of the time coordinate locate an event before the experiment started. Sometimes the solution to a problem will include negative values of one or more coordinates. Negative values for spatial coordinates indicate that the object moved in the opposite direction of that expected when the coordinate system was defined. Similarly, negative values of the time coordinate indicate events that would have happened before the experiment began. Only quantities with dimensions of mass are constrained to be positive.
The simplest and most common relationships between two variables will be a linear one. A variable y is a linear function of a variable x if y (a x) = a y (x). The graph of such a function is a straight line. When two variables are linearly related, we say that the dependent variable "scales with" the independent one. For instance, metabolic processes usually scale with the surface area of the organism, and not (as one might be inclined to think) with its mass. Pharmaceutical prescriptions are computed according to weight (which we will see scales with mass) only because weight is much easier to measure than surface area.
It is not always clear how many independent variables are necessary to describe a system. This question is often interpreted graphically as "how many axes do I need?" In many cases, the graphical version of this question is misleading. For instance, we need a two-dimensional plane in order to draw a circle. The circle, however, is a one-dimensional object: any point on a given circle can be specified by a single coordinate (ie., angle), once we have determined the origin of the coordinate. Similarly, any point on a cylinder can be found by specifying an angle and a distance (from the bottom), and any point on a sphere can be specified with two angles (ie., latitude and longitude):
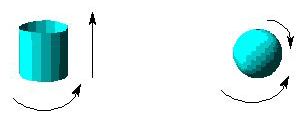
The cylinder and the sphere are surfaces that must be visualized in three dimensions, but only require two coordinates for their description. We say that they have two "degrees of freedom". A degree of freedom is simply an independent variable used in the description of a system.
The next section is about idealization, approximation and precision.
If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.
©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.