That fact that friction is incompatible with potential energy does not mean that it is not an important consideration. In fact, no real system is completely frictionless, although we will usually treat systems as if they were. For instance, if there were no friction between your shoe and the floor, you could not walk! The friction in this case is a force in the opposite direction of your movement which keeps you from slipping.
Friction often presents itself as drag, when an object is moving through a fluid medium. It is a force proportional to the object's velocity, but opposite to the direction of motion:
Here b is the "drag coefficient", with dimensions of mass over time. The drag coefficient depends on the radius and shape of the object and the viscosity ("stiffness") of the medium. For a sphere of radius r, the drag coefficient is
where h is the viscosity of medium in g / cm s. For other shapes, we multiply by a "shape factor " b / b 0 which depends on the shape of the object. So our usual procedure will be to start with the volume of an object, assume it is a sphere and compute its radius and b 0, and then multiply by its shape factor to obtain its drag coefficient. For instance, for a rod-like molecule such as Immunoglobulin G:

the shape factor is approximately 1.5. If its volume is 2 x 10 -19 cc and it is falling through a fluid of viscosity 0.02 g / cm s, the radius of an equivalent sphere would be
The drag coefficient of an equivalent sphere would be
and the drag coefficient of the molecule would be
We can also write the drag coefficient of a substance in terms of the temperature and the "diffusion constant" of the substance:
Here k = 1.38 x 10 -16 ergs / K is the Boltzmann constant, T is the temperature in Kelvin (which is the temperature in Celsius + 273.15) and D is the diffusion constant in cm 2 / s . The diffusion constant measures the rate at which something diffuses through a medium; it depends on the substance, the medium and the temperature. In this form, the shape and viscosity information is "hidden" in the diffusion constant.
Consider an object slowly sinking in a swimming pool. It sinks due to the attractive force of gravity:
(here the velocity is considered negative, and g = - 9.8 m / s 2). Opposing gravity, however, is the buoyant force of the water, which attempts to raise the object. The buoyant force is equal to the weight of the fluid displaced by the object:
Here v is the specific volume of the object (volume per unit mass), r is the density of the medium, and g is the gravitional acceleration. Thus m v gives the volume of the object, and r g gives the gravitational force per unit volume of the fluid. Since g is negative, the minus sign indicates that the buoyant force is directed upwards.
Equating the sum of the forces due to gravity, buoyancy and drag to the mass times the acceleration:
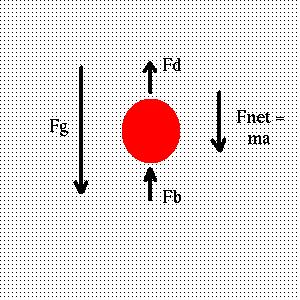
we find
or
or
Given the object's mass, specific volume and drag coefficient (m, v and b), as well as the acceleration due to gravity and the density of the fluid (g and r), we could solve for the acceleration as a function of velocity, or vise versa. For instance, we can see in the case of the swimming pool, that if the specific volume of the object is greater than 1 cubic centimeter per gram, the object will float (since r = 1 g / cc for water, and V = 0 when the object is placed on the water, the acceleration will be positive).
Since the acceleration is the time rate of change of velocity, the equation can be written in terms of the velocity alone:
This means (borrowing a result from the calculus) that the equation has a solution whose velocity is given by
For "large" times relative to m / b, that is, when
the exponential approaches zero and the velocity approaches the "terminal velocity":
It is also possible to define a "sedimentation constant"
which depends only on the characteristics of the object and the fluid, but not on the acceleration due to gravity. This is helpful because gravity is not the only external force which we might want to consider. The above results work for the object sinking in the swimming pool, or an object falling through the air, where g in both cases is due to gravity, but also for an object in a centrifuge.
A centrifuge is a rotating device used to separate materials of different mass which are suspended in a medium. An object in a centrifuge experiences a force away from the center of rotation which is often called the "centrifugal force". It is analogous to the force you feel when turning a corner in your car. Your car feels an acceleration toward the center of the circle; the resulting force ("centripetal force") keeps the car turning along the circle. Since you are, for all practical purposes, in a rotating object, you feel a force in the opposite direction. The centrifugal force is determined by the "centrifugal acceleration":
here n is the number of revolutions per second and r is the distance away from the center of rotation. If we substitute this g for the acceleration due to gravity in all of the equations involving drag, we can describe the dynamics of centrifugation. Note that for typical rates of revolution (55,000 rpm) and distances (10 cm), the centrifugal acceleration is far larger than that of gravity:
For this reason, we ignore the effects of gravity when analyzing the centrifuge.
The next section is about conservation laws.
If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.
©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.