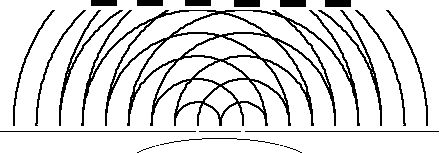
Diffraction

Diffraction is an interference phenomenon that will have some amazing consequences for us in the next section. The canonical diffraction experiment is the "double slit" experiment:

Here, a wave is incident from below on a surface with two small slits. Due to Huygens' Principle, which states that each point on a wavefront acts like a source for the next wavefront, the slits act as sources for two coherent waves. These waves interfere, resulting in a pattern of (in the case of light) bright and dark bands, corresponding to constructive and destructive interference, respectively.

For any given point on the other side of the incident wave, we have the following geometry:

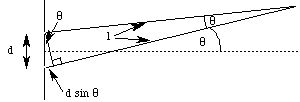
(The angles are approximately equal, as are the hypotenuse and adjacent sides of the large triangle, if the angle is small. This is true since the length is usually much greater than the distance between the slits.) The difference in length of the two rays from the slits to their point of intersection is d sin q. When this length difference is an integral number of wavelengths:

the waves are in phase, and we have constructive interference and a bright spot at the point of intersection. When this length difference is a wavelength times an integer plus one half:

the waves are p radians out of phase, and we have destructive interference with a dark spot at the intersection. If we place a screen at a fixed distance from the slitted surface, we find a pattern of light and dark bands whose intensity varies as follows:

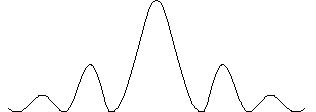
For constant wavelength, an increase in d moves the maxima closer together (the angle must decrease for a given m) and washes the pattern out; for a constant slit separation, increasing the wavelength spreads the pattern into a continuum (the angle must increase for a given m; for large enough wavelength, the condition for a maximum cannot be met). These aspects will be very important in the next section.

The next section is about matter waves (!).

• Table of Contents
• Symbols and Abbreviations
• Biophysical Chronology
• Index:
  A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.

©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.