Consider a lump of clay. We can stretch it, squeeze it or twist it. In terms of physics, we say that we apply "tensile", "compressional" or "torsional" forces, respectively. In order to quantitatively describe our fun, we define the "stress" which we apply to the clay across any cross section of it as the force per unit area. Note that these dimensions are those of pressure, and are equivalent to energy per unit volume ("energy density"):
The resulting "strain" (deformation) which the clay experiences is defined as the fractional extension perpendicular to the cross section we are considering. For instance, when stretching a cylindrical piece of clay of radius 1 cm, with a force of 100 dynes, the stress is 100 / p dynes per square cm. The cross section is a circular cut perpendicular to the force we applied to the clay, and the strain is parallel to the force. If its initial length was 10 cm, and it stretched an additional 2 cm, the strain which it experienced was 2 cm / 10 cm = 0.2. Note that the strain is dimensionless. Note also that we did 200 ergs of work (100 dynes times 2 cm extension) to stretch the clay.
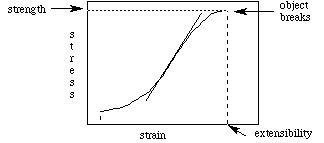
The graph of stress versus strain for a material is a veritable cornecopia of information:

The slope of the curve at any point is called the "Young's Modulus", and has dimensions of force over area. It's numerical value is indicative of the "stiffness" of the material: smaller values indicate that less stress is required for more strain. Likewise, larger values of Young's Modulus indicate that more stress is required for a given strain. Note that strain may be tensile, compressive or torsional; in general, the stress versus strain curve will differ for each material, and for each type of stress. The "strength" of the material is the maximum value of the stress before breakage. The "extensibility" is the maximum value of the strain before breakage. The "toughness" is the area under the curve between the vertical dashed lines, and is equal to the energy required to break the object. The partial area under the curve up to a given strain (less than the extensibility) is the "work of extension".
Let us revisit the collision in the first section of this chapter. Assume for a moment that the driver's head had a mass of 5 kg, and that the area of that portion of the head which hit the windshield was 25 cm 2. The compressive strength of bone is about 16 x 10 7 Pa (N / m 2). From the definition of pressure as the force per unit area, we find that the force on the head required to fracture the skull would be 400,000 N (remember to convert the area from cgs to SI units!). This implies an acceleration of 80,000 m / s 2 (from F = m a), and if the driver's head came to rest in 3 ms, the inital velocity would have to have been 240 m / s!
As a further example of stress and strain, consider a spring. We will treat the spring as a one dimensional object, so the only stress will be extensional (or compressional, which will be the negative of extension), and the units will be force per unit extension. Within a range of extension, the spring obeys "Hooke's Law", which states that Young's Modulus is a constant: the stress versus strain curve is a straight line:
where k (which is positive) is Young's Modulus, here called the "spring constant" (with dimensions of force over length), and Dx is the amount of extension. The negative sign indicates that the force is in the opposite direction of extension: if you extend the spring, the force tries to restore it to its original length. Likewise, if you compress the spring (Dx < 0), the force attempts to expand the spring, again to its original length. The area under the curve is
which gives the work of extension, or alternatively, the amount of potential energy stored in the spring. We will return to this model when we deal with arterial walls, which we will treat as springs.
Finally, we mention that the stress versus strain curve is not necessarily the same during the relaxation of stress as it was during the loading (application) of the stress. This phenomenon is called "hysteresis", and the ratio of the area under the relaxation curve to that under the loading curve (for a given strain) is called the "resiliance" (usually expressed as a percentage).
The University of Michigan maintains some tables of physical properties of biomaterials which may be useful.
The next section is on angular quantities.
If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.
©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.