The Human Cardiovascular System

While fluid systems obey the same "laws" of physics as point particles, their aggregate behavior is qualitatively different. That is, when considered as a whole, the fluid has additional properties which point particles do not. We have already seen two of these properties, density and viscosity. We will explore these and other fluid properties in this chapter.

Our model of a fluid system will be the human cardiovascular system. We will, as always, treat it in very elementary terms, so that the analyses we do are tractable.

Perhaps the most important characteristic of our treatment of the human cardiovascular system is the assumption that it is a closed system. That is, we will assume that the amount of fluid is a constant. This is not exactly true in reality, for fluid can pass through the membranes of the blood vessels in response to changes in the concentrations of electrolytes in our body. This process is called "osmosis". In addition, we can, of course, be injured and bleed. We will ignore these details, and by doing so will be able to apply a conservation principle to the system: what goes into a junction of blood vessels also comes out of that junction.

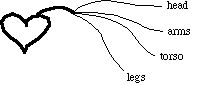
The other critical idealization we will make concerns the structure of the system. For us, the human cardiovascular system looks as follows:

1. Oxygenated blood is pumped from the left ventricle of the heart into the aorta. The ventricle is one of the four chambers of the heart, and the designation "left" is relative to the patient. The aorta is the vessel which connects to the output of the heart.

2. From the aorta, the blood enters the arteries. Both the aorta and the arteries have walls which expand and contract with the pumping of the blood, and they therefore act as auxilliary pumps, and as pressure resevoirs. We will treat the arteries as if they all connect to the aorta:
   

   while in reality they branch out from each other at various points:

   

3. From any given artery, the blood flows into arterioles. The arterioles are smaller than the arteries, and in addition, the body uses the arterioles to regulate the flow of blood in various parts of the body. For instance, when the body is cold, the arterioles leading to the skin will narrow, lessening the flow of blood and therefore of heat to the skin. Likewise, the arterioles leading to the digestive system expand while digestion is taking place, to increase the efficiency of that system. We will treat the arterioles as if they all connect directly to an artery on their "leading" end (the end the blood enters).

4. From an arteriole, the blood enters one or more capillaries. The capillaries are extremely small; in reality, they are so small that the red blood cells slide through one at a time, and the blood can no longer be considered to be a homogeneous fluid with a well-defined viscosity. We will ignore this detail. In the capillaries, the oxygen carried by the blood is used by the body, and the blood which leaves the capillaries is called "deoxygenated". Blood flow in the capillaries (and all of the way back to the heart) is smooth; that is, the pulses of the heartbeat have been smoothed out and the blood flows continuously with a constant pressure:
   

   and velocity:

   

5. Many capillaries feed into one venule. For our purposes, the only distinguishing characteristic of a venule is its relative size. It is larger than a capillary, and smaller than a vein. In reality, the subsystem of arterioles, capillaries and venules forms a complicated mesh of interconnections, but we will ignore those details.

6. Many venules feed into one vein. At this point, the blood has lost so much pressure to dissipation (below) that it can barely make its way back to the heart. The veins have one-way valves, which prevent the flow of blood away from the heart, and the movement of the body's muscles help to pump the blood toward the heart. We will of course ignore this detail. So again, for us the only distinguishing characteristic of a vein is its size.

7. All of the veins connect to the vena cava, which is the entry for deoxygenated blood into the heart.

For our purposes, we will treat this as the closed system under consideration. This means that we are going to ignore the pulmonary subsystem, which pumps deoxygenated blood from the heart to the lungs, and re-oxygenated blood back to the heart for entry into the system we described above. It also means that we have another "conservation" principle available to us: the sum of the pressure drops in the various vessels must equal the pressure applied to the system by the heart. Since we think of pressure as an energy density, this is really just a way of saying that the energy of the blood is equal to the work done against dissipation.

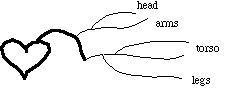
From the above simplified description of the human cardiovascular system, we can deduce the other major idealization we need: the system is purely heirarchical. That is, we assume that there are no interconnections and branchings between different types of vessels:

All arteries connect to the aorta at one end and to arterioles on the other. All arterioles connect to an artery on one end and to capillaries on the other. All venules connect to capillaries on one end and a vein on the other. And all veins connect to the vena cava. This is a gross simplification of the actual system, but it is a necessary one if we are to be able to treat the system at all quantitatively.

As the heart beats, the blood pressure in the aorta varies from the "systolic" (maximum) pressure, which occurs as the ventricle pumps blood into the aorta, to the "diastolic" (minimum) pressure, which occurs as the ventricle is filling. For a healthy person of average build, the blood pressure is often quoted as "120 over 80", which means that the systolic pressure is 120 mmHg (millimeters of mercury, that is, the increase in height of a tube of mercury due to the pressure) and the diastolic pressure is 80 mmHg. Expansion and contraction of the arterial walls, as well as dissapation from viscosity (see below), acts to reduce the pressure variations as the blood moves away from the heart. In certain instances, we will ignore this "pulsatile flow", and assume that the pressure is a constant within any given category of blood vessel.

For instance, we can compute the power output of the heart as the product of the pressure times the flow (volume per unit time). If you have six liters of blood and it circulates every minute, the flow rate is 100 cm ³ / s. If the pressure averages 133,000 dynes / cm ² (ignoring pulsatile flow), then the average power output is 13,300,000 ergs / s or 1.33 Watts. This may not seem like much, but consider the amount of energy produced by your heart in a day (86,400 s). This is approximately 115,000 J, which is the energy the average (70 kg) person would have after falling from a 550 foot tall building!

There is another pressure variation within the body which occurs when one part of the body is at a different elevation than another. This is called "hydrostatic" pressure, and arises because of the gravitational potential energy of the blood. Essentially, blood that is at a higher elevation has greater potential energy, and it "pushes down" on the blood at lower elevations. In fact, we will often think of pressure as an energy density (energy per unit volume), so we can think of the hydrostatic pressure as a gravitational potential energy density. The hydrostatic pressure difference due to a difference in height is given by

where r is the density of the fluid (which for blood is 1.05 g / cm ³), g is the acceleration due to gravity and Dh is the difference in height. If we use cgs units, g = 980 cm / s ², Dh is measured in cm and the pressure is then in dynes / cm ². We will usually ignore the hydrostatic pressure, by assuming that our patients are lying down.

For the purpose of illustrating the units we will be using, however, let's look at the hydrostatic pressure differences in a typical person. We quoted above a healthy diastolic pressure of 80 mmHg. The conversion from mmHg to dynes / cm ² is

If the diastolic pressure at the aorta is 80 mmHg, what is the pressure in the neck 20 cm higher, and at the top of the legs 70 cm lower? Converting to cgs units, the pressure at the aorta is 106,640 dynes / cm ². This indicates the utility of the more practical medical unit of mmHg. The hydrostatic pressure differences are 20,580 dynes / cm ² for the neck and 72,030 dynes / cm ² for the legs. These differences convert to 15.4 mmHg for the neck and 54 mmHg for the legs, indicating a pressure variation of almost 70 mmHg over an approximately one meter range of elevation. The resulting pressures are 64.6 mmHg in the neck and 134 mmHg in the legs. The measurement of blood pressure is usually made in the upper arm since it is at approximately the same elevation as the aorta.

The next section is about the nature of fluids.

• Table of Contents
• Symbols and Abbreviations
• Biophysical Chronology
• Index:
  A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.

©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.