The Nature of Fluids

The term "fluid" applies to both liquids and gases, and indeed to some things which we think of as solids (ie., glass). The essential differences between fluids and solids can be summarized as follows:

  1. Fluids are shapeless. In more technical terms, we say that fluids do not resist being "sheared". That is, it is relatively hard to bend a solid object, but a fluid "splashes" under the same force.

  2. When a force is applied to a fluid, the pressure increases, but whereas the force is directional, the pressure is omnidirectional. Consider the force applied to the surface of a glass of water by the atmosphere. That force is downward, but the resulting pressure is felt throughout the water. If we measure the hydrostatic pressure at any given depth, it is the same on all sides of the measuring instrument. In cases where we can ignore hydrostatic pressure and dissipative losses, the omnidirectionality of pressure is equivalent to conservation of energy: the energy density (pressure) is a constant throughout the fluid.

  3. Fluids are "viscous" (but not necessarily viscious!). While fluids do not resist shear, they do resist changes in the rate of change of shear. The more viscous the fluid, the greater its resistance to changes in the rate of shear: colloquially, we say the fluid is "syrupy". In cgs units, viscosity is measured in Poise: the viscosity of water is .01 Poise (dyne s/cm 2 = g / cm s), and the viscosity of blood is .04 Poise.

  4. Fluids flowing past a solid surface obey the "no slip condition". That, is the velocity of the fluid at the solid surface is zero. This may seem surprising, until you recall that your dishwasher often does not clean well when, for instance, the dishes are coated with cheese. The no slip condition means that the water by itself is not as effective as scrubbing with a solid object, and so many of us wipe the dishes before putting them in a dishwasher. Since the velocity of the fluid is nonzero elsewhere, the no slip condition implies that a "velocity gradient" exists in the flowing fluid. In a pipe (or blood vessel), the velocity profile across the diameter is essentially parabolic:

    v = DP (a 2 - r 2) / 4 l h,

    where DP is the pressure difference between the "head" (upstream) and "tail" (downstream) ends of the pipe, a is the radius of the pipe, r is the position along the diameter from the center, l is the length of the pipe and h is the viscosity of the fluid. For a cross section of the pipe, the velocity gradient has circular symmetry:

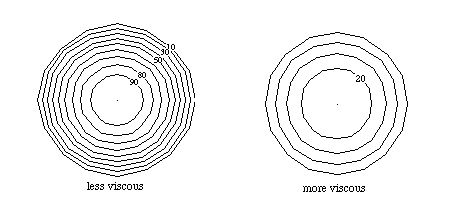
    The fact that the velocity is constant on each circle leads us to think of the fluid as flowing in concentric "sheets", but in fact the velocity is a smooth function of distance from the center. For higher viscosity, the velocity gradient is shallower. Essentially, viscosity opposes the existence of steep velocity gradients. The larger the viscosity, the "gentler" is the shape of the parabolic velocity gradient, and the velocity is more nearly constant across the section.

  5. Fluids are subject to turbulence. Smooth flow is called "laminar", implying that layers of fluid flow past each other in a sheet-like fashion. The flow is turbulent when eddies and vortices occur. Fluids lose energy through dissipation in both types of flow. During laminar flow, the viscosity causes "frictive" losses (due to "friction") between the sheets of fluid: the fluid resists changes in the velocity gradient, and that costs energy. In turbulent flow, energy is required to create the eddies and vortices, resulting in an energy loss by the fluid as a whole.

The next section is about Poiseuille's Law.

If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.

©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.

Please send comments or suggestions to the author.