
We can model an axon by the following electrical circuit fragment:

The vertical RC components represent the axon membranes at the Nodes of Ranvier: they behave as leaky capacitors. The top row of resistors corresponds to the resistance of the intracellular fluid, and the bottom row to that of the interstitial fluid. We will assume that all of the horizontal resistances are the same. The dots at each end signify that the circuit continues indefinitely in both directions. Note that the rest potential of the membrane corresponds to a charged capacitor, and that the action potential corresponds to the discharge of the capacitor at that node.
We first have to turn this circuit fragment into a complete circuit. To this end, we will ignore the capacitors both up and down stream from the central node, since minimal current is flowing there during the action potential at that node. This leaves us with a large number of resistors to simplify. To do that, we will use the "infinite axon approximation", since 1) we have approximate lateral symmetry (the axon looks the same along its entire length, and we pretend to be in the middle) and 2) the width of the Node of Ranvier is much smaller than the length of the axon. This allows us to modify the fragment into a complete circuit:
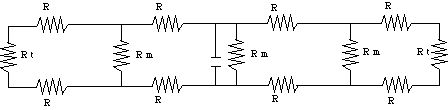
R is the resistance of the fluid (12 KW), R m is the membrane resistance (which is 200 KW during the action potential) and R t is the resistance of the rest of the axon. Since the axon is "infinitely long", we can replace the outer loops with R t:
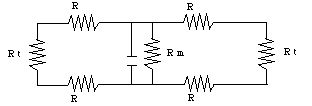
Equating the original "resistance loops" to R t gives us
or
or (using the quadratic formula)
Now we can replace ALL of the resistors with a single resistor, and compute the RC constant for the circuit:
and
With our values for the various resistances, we find that R t is 58 KW and R eq is 34 KW. C is around 1400 pF; this is larger than one would expect from the capacitance per unit length quoted above, noting that the nodes are 1 micron wide. This is due to the decreased leakage, due in turn to the myelin sheath. The result is a time constant in the order of 81 ms, which is consistent with the firing times in Section D.
To find V t (the voltage at the next node) when the action potential peaks, we ignore C so that I t is equal to one half I m (C is totally discharged at V m = 70 mV above rest potential, and therefore represents an unconected wire: an "open circuit"). Using Ohm's Law , we have
which gives us a value for V t of - 64 mV when Vm reaches 0 mV. This discrepancy with the results of the "Axon Propagation" Mathematica notebook corresponds to the difference between a Gaussian and an exponential dependence of charge on time (the Gaussian rises more quickly).
The next chapter is about magnetism.
If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.
©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.