Very few organisms are biomagnetic. While magnetism is quite important in the medical application of Magnetic Resonance Imaging, our primary reason for learning about magnetism is to set the stage for the next chapter on atomic physics. Ordinary "ferromagnetism", while interesting, lies outside the scope of this text.
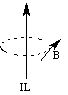
Magnetic forces are analogous to electric forces, and we use the same field model to understand them. In the case of magnetism, there is a force between currents, and so current "elements" (a length of current) are the sources of the magnetic field. The magnetic field due to a (vector) current element IL is
where m is the "magnetic permeability" and m 0 = 4 p x 10 - 7 N / A 2 (an exact value) is the magnetic permeability of the vacuum. The factor "(L x R)" is the "cross product" of the vector L with the vector R (pointing to the field point). The effect of the cross product is to make B perpendicular to both L and R. The direction of B at any point is tangent to a circle centered on and perpendicular to the current element:

We say that B is an "axial" vector field because of its axial (cylindrical) symmetry with respect to its source. As we will see below, the orientation of the B field around the source current (clockwise or counterclockwise) is determined by the direction of the current (the flow of positive ions). You can view the magnetic field (in black) due to a current (in red) from different angles in 3D in a quicktime animation (120K).
The magnitude of the magnetic field is
where q is the angle between the current element and the position vector of the field point. The SI unit of B is the "Tesla", or N / A m (a very large unit); the cgs unit is the "Gauss", or dyne / A cm (10 - 4 T; the Earth's magnetic field is typically a fraction of a Gauss).
The force exerted by B on a length l of test current I is
where q is the angle between B and the test current; therefore if B is parallel to I, F is zero. The direction of F is perpendicular to both B and the test current. This situation is quite different from that of the electric and gravitational forces, which act along a vector parallel to their respective fields (pointing from one source to another). It is as if pushing someone (analogous to the magnetic field) would not exert a force unless they were already moving (analogous to the moving charges in the current), and on top of that, a sideways push while they were running past you would cause them to rise into the air! In further contrast with the case of the electric force, parallel currents attract and antiparallel currents repel. You see that the business of magnetic fields and forces is inherently three dimensional, and is quite counterintuitive. We will use a set of "Right Hand Rules" ("RHR") to get the directions straight.
We will use the same configuration and test model that we used for electric fields. The configuration current is assumed to be infinitely long so that we do not have to worry about nonsymmetrical effects near the ends of the current element. The test current is finite. Imagine a cylinder which is concentric with the source (configuration) current. The magnetic field is everwhere tangent to this cylinder, and its strength decreases as the distance from the current (radius of the cylinder) increases. The direction of B is given by the first right hand rule:
1. Point the thumb of your right hand along the current; your curled fingers will show the direction of B.
The direction of the force is also given by a right hand rule:
2. Point the fingers of your right hand along the test current, with your palm facing in the same direction as B; your thumb shows the direction of the force experienced by the test current.
As always, B and F superpose, so that B due to several configuration currents is equal to the sum of the B fields of each. Also note that since the field is axial and decreases as the distance from the configuration current increases, test currents in magnetic fields often rotate.
For example, think of a configuration current pointing upwards in the plane of the page, with a test current pointing out of the page:
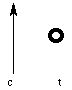
Here the open circle indicates a current coming out of the page (the "point" of the vector); a circle with an "x" in it indicates a current going into the page (where you only see the "tail" of the vectors, like the feathers on an arrow). The B field due to the configuration current is on a cylinder coaxial with it:
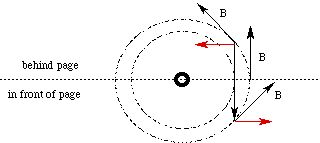
and going into the page (RHR 1) at the point on the page where B and the test current meet. Therefore at the page, the force is zero: B and the test current are antiparallel (q is p radians or 180 degrees). In front of the page, however, they are not parallel: B has a component pointing to the right (in red), and so by RHR 2, the force on the test current is up. Behind the page, B has a component pointing to the left, and so the force on the test current is down. Therefore, the test current will rotate upward (in front of the page) about an axis in the page:
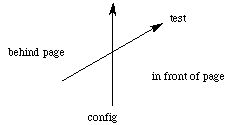
Similarly, consider the following currents:
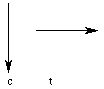
Since the test current lies in the plane of the page, B at the test current (due to the configuration current) is everywhere perpendicular to it, pointing out of the page. Therefore, the test current experiences a downward force along its length. Since B decreases with increasing distance from the configuration current, however, the magnitude of this force will be smaller on the right side of the test current than it is on the left. Therefore, the test current will move down, but the right side will rotate up as it does so:
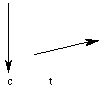
Finally, consider the following currents (with the B fields due to the configuration currents shown):
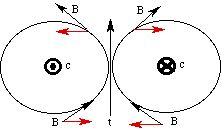
Since the test current is equidistant between the configuration currents, the horizontal components of the B fields are equal and opposite. Therefore, the net B field is vertical and hence parallel to the test current: there is no force exerted on it. Of course, if the test current were not exactly in the center of the configuration currents, the horizontal forces would not cancel and there would be a rotation.
We have seen that magnetic fields and forces force us (pun intended) into the world of three dimensional vectors. There are a set of mathematical rules to deal with them algebraically, and even a "magnetic potential" (which happens to be a vector and requires some substantial calculus to use), but for our purposes, a good qualitative understanding of the right hand rules will be sufficient:
The next section is about mass spectroscopy, current loops and spin.
If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.
©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.