In Section A, we noted that the speed of sound in air depended on both the molecular weight and the temperature of the air. We also noted that the speed of light depended on both the electrical permittivity and the magnetic permeability of the medium. It is a general characteristic of waves that their phase velocity depends on the medium in which they travel. While we will shift our attention to light, we note that everything we will be discussing still applies to other types of waves.
Nature is fundamentally "lazy". We have seen that particles in a potential field will move to the position of least energy and that electricity takes the path of least resistance. Waves are no different. They follow the path of least total elapsed time. The consequence of this is that their path changes when they enter a different medium (with a different characteristic phase velocity). These "lazy rules" which nature follows are all specific examples of the "principle of least action". The action is defined as the integral of the difference between kinetic and potential energy with respect to time. Everything in nature behaves the way it does because it follows the path of least action. Another of nature's deepest mysteries is why this must be so.
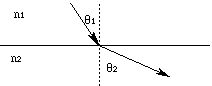
If we define a light "ray" as the "arrow" perpendicular to a moving wave front, we can conveniently examine the changes in path across the boundary of two media. That change in path is known as "refraction", and is expressed in terms of "Snell's Law":
where n is the "index of refraction" of the medium. The index of refraction is the ratio of the phase velocity in a standard medium, ie., air for sound or vacuum for light, to the phase velocity in the medium; it is always greater than one. The angles are measured from the normal to the interface between the two media:

Note that for any angle greater than the "critical angle"
Snell's Law is not applicable; you get "total internal reflection", which means that the ray (and hence the wave) does not cross the boundary.
If n 1 is the same as n 2, Snell's Law describes reflection from a mirrored surface: the reflected angle equals the incident angle. Some representative indices of refraction are:
for sound,
- n = 1 in air;
- n = .06 in glass;
- n = .23 in water;
- n= 6.1 in rubber;
for light (of wavelength 589.3 nm),
- n = 1 in a vacuum;
- n = 1.0003 in air;
- n = 1.333 in water;
- n = 1.336 in vitreous humour (inside the eye);
- n = 1.413 in the eye's lens;
- n = 1.52 in crown glass;
- n = 1.61 in flint glass, and
- n = 2.42 in diamond.
We can use Snell's Law to understand the focussing of images by lenses, including the lens of the eye. We categorize several types of lens:

For each of these lens types, we can specify a "radius of curvature" for each curved face. That radius is the radius of a circle which would have that face as an arc. We also define an "object length" (O, the distance from the center of the lens to the object which is to be seen), an "image length" (I, the distance from the center of the lens to the place where the image is to be viewed) and a "focal length" (f). The focal length is the distance from the center of the lens to the "focal point"; light rays from a sufficiently distant object will all be approximately parallel as they enter the lens, and will converge at the focal point:
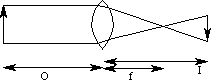
The object is of course on the left in this picture, and the image is on the right. Note that the image is inverted, as it will be with a convex lens. These quantities are related by
For thin lenses in air with radii of curvature r 1 and r 2,
(light enters the r 1 side and exits the r 2 side; r i is considered positive if its center of curvature is on the right; if either side is flat, r is assumed to be infinite). Note that the focal length will be negative for concave lenses, since the focal point is actually on the same side of the lens as the object:
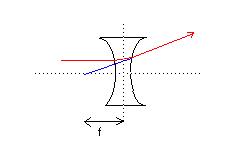
We can also define the strength of a lens (in "diopters", if f is measured in meters) as
and vision correction is then a simple matter of addition:
This fact that the strengths of lenses add also allows us to construct one type of lens from others. For instance, a plane-concave lens with exit radius of curvature 10 cm can be constructed from a plane-convex lens with exit radius of curvature 8 cm and a concave lens with entry radius of curvature 8 cm (to "fit" the plane-convex lens) and exit radius of curvature 10 cm. The strength of the composite lens is simply the sum of the strengths of the component lenses.
We define the magnification of a lens as
which is effectively the ratio of image size to object size.
A ray of light as it traverses corrective lenses and the eye is refracted:
- as it enters the corrective lens;
- as it exits the corrective lens;
- as it enters the cornea;
- as it exits the cornea into the eye's lens;
- the width of the lens (and hence the radii of curvature and the focal length) is controlled (within the elastic limts of the lens) by muscles which stretch the lens "vertically";
- and finally the ray is refracted as it exits the eye's lens and enters the vitreous humour.
Note that the focal point should be just short of the retinal surface; if it is too close to the eye's lens, the eye is "near-sighted" (and requires a divergent, "defocussing" corrective lens); if it is on the retinal surface, the world appears as a bright point of light; and if it is behind the retinal surface, the eye is "far-sighted" (and requires a convergent, focussing corrective lens).
Check out the information on vision at York University, particularly the demonstrations on visual acuity.
The next section is about diffraction.
If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.
©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.