9-1. The smallest object that can be seen by any instrument depends on the smallest distance between two points that that instrument can differentiate. That distance defines the "resolution" of the instrument. In general, that distance is limited by the type of waves used by the instrument to "see", and is approximately equal to their wavelength. What is the smallest object which can be seen using light waves? using x-rays?
9-2. Suppose that your eyes were sensitive to microwaves instead of light. Assume that the frequencies you are sensitive to are on the order of one billion Hertz. What is the smallest object you can see? What does this tell you about radar?
9-3. Medical ultrasound uses frequencies on the order of 20 MHz. If the speed of sound in tissue is 1500 m / s, what is the smallest object which can be detected? If the penetration distance is approximately 200 wavelengths, how deep can this instrument penetrate?
9-4. The upper frequency limit of a person's hearing is partially determined by the size of their eardrum (tympanic membrane). If the wavelength equals the eardrum diameter at the upper limit, how big is your eardrum? If you don't know the upper frequency limit of your hearing, assume that it is between 16,000 and 20,000 Hz. Is your answer reasonable? Assume room temperature air.
9-5. The modes excited on a guitar string when it is plucked depend on where it is plucked and on the effective length of the string. The point of plucking is a maximum of the amplitude, so that only those modes which have a maximum there are generated. Use the "Sound Modes" Mathematica notebook or the "Waves" Java program to determine where to pluck a guitar string (for a given length) in order to excite each of the first six modes of the string. For each of these locations, which harmonics will sound?
9-6. Your ear canal is a tube approximately 2.8 cm long, and is open at one end. What is the natural resonating frequency of your ear canal (the fundamental)? Why do you think it has this value?
9-7. Research the intensities of sound for normal conversation, various loudnesses of music, several loud mechanisms (ie., a jackhammer and a jet aircraft), and the thresholds for pain and permanent damage. For each, compute the relative increase in distance between you and the source necessary to carry on a normal conversation in the presence of that noise.
If you would like to do this problem without a calculator, note that 10 is approximately 2 3.33; this means that log(x) = 0.3 log 2 (x), and you can use the approximations (with base 2 instead of 10) you tried in chapter 7.
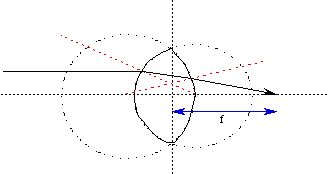
9-8. Use the thin lens equation to compute, and make drawings using Snell's Law to confirm, the focal lengths of all of the lens types, with n = 1.52, | r 1 | = 5 cm and |r 2 | = 6 cm . Draw the lenses as thin as possible with room to draw the ray diagrams:

Have your light ray enter 1/2 to 2/3 of the way up from the center of the lens. The red lines are radius lines of the circles used to draw the lens faces; they define the normal to the interface for the purpose of measuring the angles for Snell's Law.
9-9. The lens in your eye is effectively a convex lens with a focal length of approximately 22 mm. Assuming that you wish to be able to focus on objects 10 cm away, what strength corrective lens do you need? Assume that the distance from the center of your eye's lens to the retina (the image distance) is 22.5 mm for this and the next two problems.
9-10. Near-sighted people can focus close but not far away. If my distance of farthest focus is 15 cm, what strength corrective lens do I need to be able to focus arbitrarily far away?
9-11. Far-sighted people can see far away but cannot focus on close objects. If my distance of closest focus is 40 cm, what strength corrective lens do I need to correct it to 6 cm?
9-12. Compute the velocity, wavelength and angular momentum of an electron in the n = 1 state of Hydrogen. Is Bohr's quantization condition satisfied? Is it meaningful to speak of the velocity of a standing wave?
9-13. Compute your Compton wavelength as you are walking to class. Is it a meaningful quantity?
9-14. It is thought that the proton pumps in your mitochondria (which we discussed in the last chapter) utilize tunneling on a regular basis. Compute the average kinetic energy of a proton at body temperature, and from that compute its Compton wavelength. How does it compare with typical membrane thicknesses?
9-15. Your body is made up of atoms, which are all essentially complex collections of mutually interacting standing waves. When describing those waves we are limited by Heisenberg's "Uncertainty Principle":
This means that if we attempt to localize a wave to a very small area, its momentum will be arbitrarily large and we won't know where it went. If we make its momentum very precise, it will spread out to cover the entire universe!
Armed with this information, criticize the various "transporter" or "teleportation" technologies which appear regularly in science fiction.
9-16. What muscle movements are required for your eye to focus on far-away objects? on nearby objects? On what does the magnification of your eye's lens depend? How does that differ from the lens in your glasses?
If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.
©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.