Particle Interactions

Our picture of elementary particle interactions so far must reflect what we know about charges: quarks interact electromagnetically and strongly, since they have both electric and color charge. The left handed ones, like all doublet members above, also interact "weakly". The weak interaction allows the transformation of one doublet member into the other. For instance, an up quark can change into a down quark via a weak interaction. This should be impossible, since none of the doublet pairs have the same mass, and we have said that mass is conserved! However, the equivalence of mass and energy, as expressed in Einstein's famous formula

allows us to create matter from energy and visa versa. The weak charge denotes one of the two members of a doublet. Each doublet is sort of like two sides of a coin, but you can only see one side at a time. The weak charge tells you which side (member) you have; as this implies, the right-handed particles do not interact weakly.

Since quarks have mass, they also act gravitationally (albiet very weakly!). So left handed quarks participate in all four known fundamental interactions: electromagnetic, weak, strong and gravitational. Right handed quarks do not interact weakly. The left handed charged leptons participate in the electromagnetic, weak and gravitational, and the neutral leptons (the neutrinos), if actually massless, participate only in the weak interaction. This may indicate a relationship between electric charge and mass; another reason the mass of the neutrino is so important to measure. The right-handed leptons only participate in the electromagnetic and gravitational interactions:

Particle	Interactions
u, d _left	strong, weak, electromagnetic, gravitational
u, d _right	strong, electromagnetic, gravitational
e^-_left	weak, electromagnetic, gravitational
n_e	weak (gravitational ?)
e^-_right	electromagnetic, gravitational

The Standard Model poses that photon-like "Gauge Bosons" mediate these interactions. The notion is that a force is felt between two charged particles when a gauge boson is exchanged between them. This finally gives us a model of "action at a distance" which fits our intuition! The term "boson" indicates that they are not fermions, and do not obey the Pauli Principle: they can be anywhere they want, no matter who is in what quantum state at the same place in the same time! Each interaction has one or more gauge bosons associated with it. The photon is the gauge boson for electromagnetism:

Boson	Charge(e)	Mass(MeV / c ²)
g	0	< 3 * 10^{- 33}

The weak gauge bosons are the W⁺, W^- and Z. For intricate reasons beyond the scope of this text, the weak gauge bosons are massive (making them "slow and weak") and two of them are electrically charged:

Boson	Charge(e)	Mass(MeV / c ²)
W⁺	+1	80,100
W^-	-1	80,100
Z	0	91,100

The strong gauge bosons are called "gluons", are believed to be massless, and are very strong, but only at certain distances (see below):

Boson	Charge(e)	Mass(MeV / c ²)
G	r-bbar	0?
	b-rbar
	r-gbar
	b-gbar
	rbar-g
	bbar-g
	(b-bbar - r-rbar)
	(r-rbar + b-bbar - g-gbar)

The "bar" denotes an "anticolor", so that for instance, absorption of an r-bbar gluon changes a blue quark into a red one, and emission of an r-bbar changes a red quark into a blue one.

While gravity is believed to be describable in terms of a gauge boson called the "graviton", we are still very far from a theory of quantum gravity which can be understood in analogy to the structures and interactions above.

What can we do with this menagerie of particles? We have found that a proton is actually a a tightly bound triplet of two up and one down quarks. Similarly, a neutron is made of two downs and one up. With this model, we can visualize radioactivity not in terms of the composite nucleons, but in terms of the elementary particles. Beta decay is actually

changing the down quark to an up quark and the neutrino to an electron (each change within a doublet caused by the transfer of weak charge). The neutron which decayed is now a proton, because it has two ups and a down. Notice the conservation of charge: the loss of a negative one charge in the form of the W boson has changed the - 1/3 charge on the down quark to the + 2/3 of the up quark. The neutral neutrino has changed to the negatively charged electron, and the neutral neutron (charge - 1/3 - 1/3 + 2/3) has become the positive proton (charge 2/3 + 2/3 - 1/3). The diagram above is called a "Feynman diagram", after the physicist who pioneered this field.

Interaction	Mediator	Strength	Range	Lifetime (s)
EM	g	1/137	long	10^{- 20}
Weak	W, Z	10^{- 5}	short	10^{- 8}
Strong	G	.1	*	10^{- 23}
Gravity	g	10^{- 41}	long	long

The general principle to note here is that the stronger the interaction, the shorter the range, and the shorter the lifetime of the particles which carry the charge of that interaction.

All of the interactions conserve momentum, energy, angular momentum, charge, type (fermion / boson) and CPT. C is charge conjugation (swapping), P is parity (spatial reflection) and T is time reversal. Electromagnetism conserves C, P, and T separately. The weak interaction conserves none separately. The strong interaction conserves C and P separately. That C and PT should be at all related is another of the fundamental mysteries: since C is an "internal" quantity (charge), while the others are related to space and time, it makes one wonder about a more meaningful relationship between the structure of particles and the spacetime they live in.

The model of interaction by the exchange of gauge bosons is home of the most accurate computation and the most accurate measurement (both of which agree!) in science:

the gyromagnetic ratio for the electron = 2.002319304376 +- 8.6 * 10^{- 12}.

While this is certainly impressive, it should be noted that the theory which makes this claim ("Quantum ElectroDynamics", or "QED") suffers from problems with infinite answers. While a scheme has been developed to get around this (called "renormalization"), one should be reminded of the problems in the simulations in problems 4-5 through 4-8. There, infinite quantities were encountered when charged particles sat on each other (r was 0). This arises from the point particle approximation, which is clearly an idealistic fiction. All of the "particles" described above are actually extended fields, and QED attempts to treat them as such. But since it is a "local" theory (which means that r can still be 0!), it suffers from that same sort of problem (as does its strong brother "QCD": "Quantum ChromoDynamics"). One must always remember that an infinite answer means the theory is no longer usable or appropriate for what you are studying. The solution is to modify the theory (as in the use of renormalization) or find a new theory which does not have these problems.

The other side to the gauge boson model for interactions makes the universe a busy place indeed. It is (essentially) a "perturbative" theory. That means that we do not know how to compute anything with perfect certainty: there is always some inaccuracy, due to the fact that we have to ignore answers smaller than some given order of magnitude. For QED, each time a photon is added to a diagram, the order increases by two. For example,

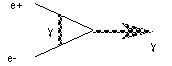
is a third order part of "electron-positron annihilation" (into a photon). Since each "vertex" (where a photon touches another particle) adds a factor of 1/137, it represents a smaller contribution to the final answer than the first order diagram. It so happens that to get the "right" answer (above), you need to include ALL POSSIBLE diagrams. This means that everything that can happen, does!