Since you are a warm-blooded animal, your body attempts to keep its internal temperature constant. Human life is only compatible with a narrow range of temperatures:
| Temperature (C) | Symptoms |
|---|---|
| 28 | muscle failure |
| 30 | loss of body temp. control |
| 33 | loss of consciousness |
| 37 | normal |
| 42 | central nervous system breakdown |
| 44 | death* |
(* by irreversible protein "denaturation", or unfolding; once their shape changes, they cease to function properly.) As we will see in the next section, you are constantly generating heat, and so your body must take active steps to lose that heat. The following table illustrates the power cost of various common activities:
| Activity | Energy Cost (Cal/m 2 hr) |
|---|---|
| sleeping | 35 |
| sitting | 50 |
| working at a desk | 60 |
| standing | 85 |
| washing & dressing | 100 |
| walking (3 mph) | 140 |
| bicycling | 250 |
| swimming | 350 |
| running | 600 |
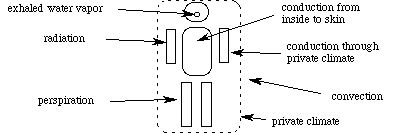
Approximately 80 % of these costs is waste heat. The other side of this coin is cold weather: your body must then work to stay warm. The mechanisms which either are used by your body or affect its function are "conduction", "convection", "radiation" and "evaporation".
Conduction is the flow of heat energy from regions of warmer temperature to regions of cooler temperature. In Chapter 4, we associated this with the electric potential (voltage), whose gradient (the electric field) was responsible for the motion of charges (current). Similarly, in Section A of the present chapter we spoke briefly about the diffusion current, which represented the motion of particles due to a concentration gradient. The three are mutually analogous, as we see in the following equation for the "heat current" (rate of heat flow):
where k is the "conductivity". Note that since the temperature occurs as a linear difference, you can use Celsius as well as Kelvin scales. The analogy to Ohm's Law is made complete by equating DQ / Dt to I, DT to V, and Dx / k A to R (resistivity corresponds to 1 / k). Note that in this analogy, R would have units of C / Watt; this is the common "R-value" of insulation. When multiple layers of insulating material are used (ie., in clothing), the "total resistance" to heat flow is just the sum of the individual resistances. Some useful conductivities are given in the following table:
| substance | conductivity |
|---|---|
| air (0 C) | .000057 cal cm / s cm 2 K |
| H 2 O (20 C) | .0014 cal cm / s cm 2 K |
| Cu | .99 cal cm / s cm 2 K |
| tissue | 18 kcal cm / m 2 hr K |
| fur/down | .36 kcal cm / m 2 hr K |
Assume that you walk at 2.2 mph on flat ground. At this speed, an average person burns 3.33 kcal / min, 80% of which must be lost in heat . Consider first the conduction of heat from the center of your body to the skin. Assuming that the average area (inside the body) through which heat is conducted is 1 square meter and that the average distance the heat must travel is 10 cm, the temperature difference necessary to maintain normal body temperture is 89K! Clearly your body cannot rely on conduction for this service! Now consider the conduction of heat away from the skin. Due to the nature of the surface of your body, it has a "private climate" about 3 mm deep through which the temperature changes from skin temperature to the surrounding air temperature. At room temperature, a person with 2 square meters of body surface area must (when nude) have a skin temperature of almost 32 C when the air is still. This is actually a pretty reasonable estimate.
Convection is the movement of heat by currents in the medium, ie., the wind. The convection current in Watts is (empirically)
when A is measured in square meters and v is the (wind) speed in m / s. Still air actually has a convection velocity of .23 m / s (called "natural convection") because warm air rises. For the body in air, convection is in series with private climate conduction. Within the body, blood convection is used to move the heat from the inside of your body to your skin. Here the area is the surface area of the capillary bed, which for the average adult male is about 160 square meters. Using the skin temperature and heat current above, we see that the blood flow must be around 2 mm / s, which is the correct order of magnitude. Since the specific heat of blood is larger than that of air, we expect the thermal current to be larger for blood, and hence the velocity to be smaller than this estimate.
Radiation is the emission of electromagnetic energy (which your body does in the infrared wavelengths). The radiation current (in Watts) is
where e is the "emissivity" (a dimensionless radiation "effectiveness", which is .97 for human skin independent of color, under equilibrium conditions), s is the "Stefan-Boltzmann" constant (5.67 * 10 - 8 W / m 2 K 4) and the temperature MUST be in K (due to the fourth power dependence; "b" denotes body, while "a" denotes "ambient", or air, temperature). In the above scenario, your body's radiation power output is only about .002 W.
When considering radiation absorbed by the skin from the sun, the emissivity (which is equal to the absorbancy) depends on frequency and therefore on skin color (we know this is not an equilibrium situation, because many people can get severe sun burns!). Using data on the reflectance of human skin as a function of wavelength (where reflectance is 1 - e), we can construct a weighted average emissivity for various skin colors (weighted by the solar power output as a function of wavelength). Using this data, caucasian skin has a weighted average e of .566, while negroid skin has a weighted average e of .838.
Evaporation is of course simply the change of phase of sweat. The rate of sweat is then related to the thermal current by the latent heat of vaporization:
At body temperature, the latent heat of vaporization of water is 580 cal / g. For short periods, you can sweat up to four liters per hour; for longer periods (up to 6 hours), 1 liter per hour is common. In addition to sweat, however, your body also loses water vapor during respiration. The volume of air which you inhale with each breath must be humidified by your body to saturation in order to be used efficiently. This vapor is then exhaled, resulting in an evaporative loss which at high altitudes can rival sweat as a cooling factor. This makes evaporation a major contributor to heat regulation, up to a point: body functions are severely limited when you have lost 10% of your weight due to dehydration.
Your body has a number of mechanisms to help it cope with cold weather. Constriction of surface capillaries is helpful when the ambient temperature is above 19 C (for a nude person). Shivering raises the average person's metabolic rate about 250 kcal / m 2 hr (relative of course to body surface area). In fact, for any well-insulated animal, evaporative losses in breathing limits the ability to withstand cold temperatures.
We can summarize the various modes of heat transfer with the following diagram:

We can use the "Body Heat" Mathematica notebook to analyze the dominant effects when your body moves from heat gain to heat loss. The notebook defines the various heat loss mechanisms and allows us to choose which ones we want to include in the model. The model corresponds to exercise on a level treadmill. We will assume that the resultant heat loss (wastage) is a parabolic function of speed, with a value of 11.2 Cal / min at a speed of 9 kph. We will further assume that your skin temperature varies parabolically from 28.2 C at an ambient temperature of 9.5 C to 37.2 C at an ambient temperature of 35 C. Finally, we will assume that you do not sweat when the ambient temperature is below 30 C, and that above 30 C the rate of sweat is proportional to the amount by which your skin temperature exceeds 30 C. These assumptions are based on studies on medical students in the mid-twentieth century. We will supplement them with an estimate of the amount of water vapor exhausted during respiration which is proportional to the rate of exercise.
Since the net heat loss or gain is a function of three variables (ambient temperature, rate of walking and wind speed), we have to analyze a three dimensional field. The slice function illustrates the parameter ranges for the three variables which correspond to your body switching from heat gain to heat loss. The other graphs show which effects dominate, and allow us to find optimum exercise conditions.
The next section is on cellular metabolism.
If you have stumbled on this page, and the equations look funny (or you just want to know where you are!), see the College Physics for Students of Biology and Chemistry home page.
©1996, Kenneth R. Koehler. All Rights Reserved. This document may be freely reproduced provided that this copyright notice is included.
Please send comments or suggestions to the author.